〔証明〕ひし形abcdの対角線ac,bdの交点をoとする。 aboと ( )において ひし形の定義から ( )=( ) ・・・1 ひし形は平行四辺形だから 対角線はそれぞれの中点で交わるから ( )=( ) ・・・2 また 平行四辺形とは、「 2組の向かい合う辺 (対辺)が、それぞれ平行な四角形 」のことを指します。 また、平行四辺形は 台形 の一種です。 さらに、平行四辺形の中には特別に名前のついている四角形があり、それが 正方形やひし形、長方形 と呼ばれる四角形のことです。 図にまとめたので確認してみてください。 平行四辺形の定義はとても重要なので、次2年生 5 図形の性質と証明 知識・技能の習得を図る問題 年 組 号 氏名 全国学力・学習状況調査 A問題 ② 2 下のように「平行四辺形の2組の向かい合う辺はそれぞれ等しい」ことを証明しました。
1
平行四辺形の定義 証明
平行四辺形の定義 証明-「2組の向かい合う辺がそれぞれ平行である四角形」を平行四辺形という.(平行四辺形の定義) この頁では平行線の性質について,1つの性質から他の性質を証明する場合を例にとって, 仮定と結論の選び方 を練習する. Step2 平行四辺形の性質をつかう! 長方形は平行四辺形の1種だったね?? ってことは、 平行四辺形の性質がつかえるってわけ。 よって、 2組のむかいあう辺がそれぞれ等しい より、 AB = DC ・・・(2) になるね。 Step3 三角形の合同条件をつかう! BCは



中2数学 平行四辺形の証明のポイントと練習問題 Examee
数学・算数 平行四辺形の証明 平行四辺形の証明において、 (1)対辺は等しい。 (2)対角は等しい。 (3)対角線は互いに他を二等分する。 という三つの証明を各々どう証明すればよいのかと聞かれて 質問No 平行四辺形になるための証明 次は、平行四辺形になるための証明を見ていきましょう。 こちらの問題は今までのものとは少し違います。 今までは、辺の長さや角の大きさが等しくなることを証明してきましたが、今回は注目する四角形が平行四辺形に・平行四辺形,長方形,ひし形,正方形の定義や性質を用いて,それらに関する図形の証明が きちんと記述できる。 知識・理解 ・平行四辺形,長方形,ひし形,正方形について,その定義・性質・そうなるための条件のそれ ぞれの意味や内容が理解できる。
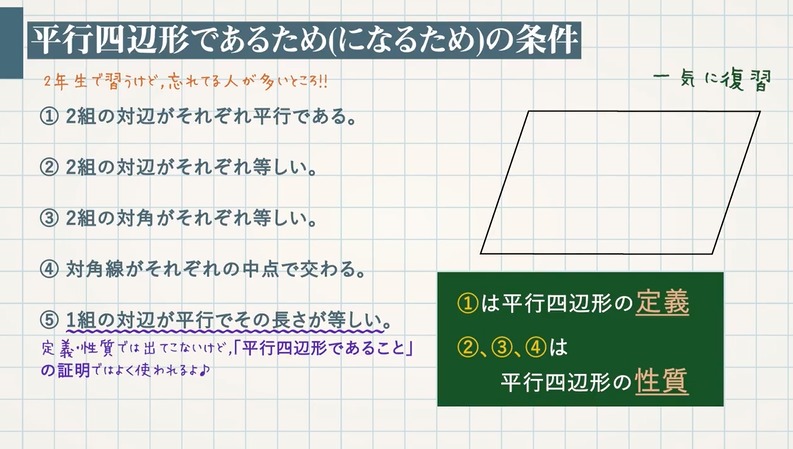
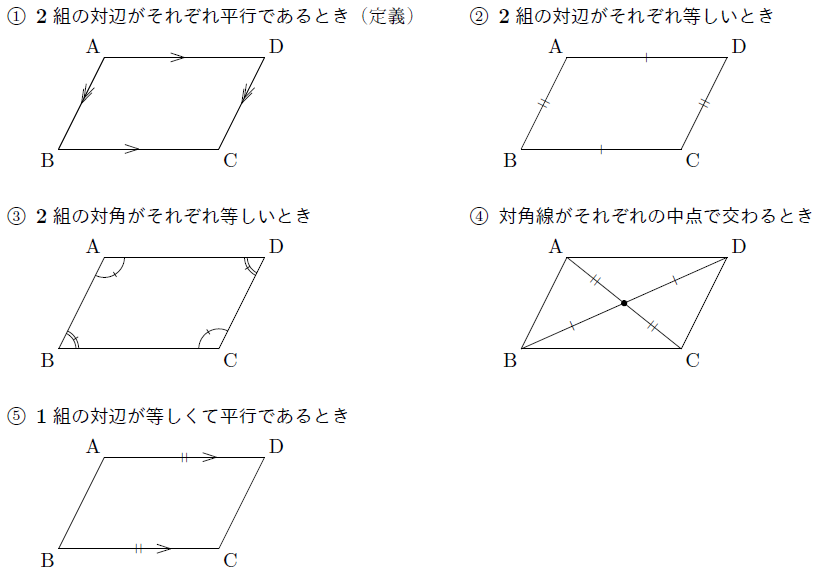
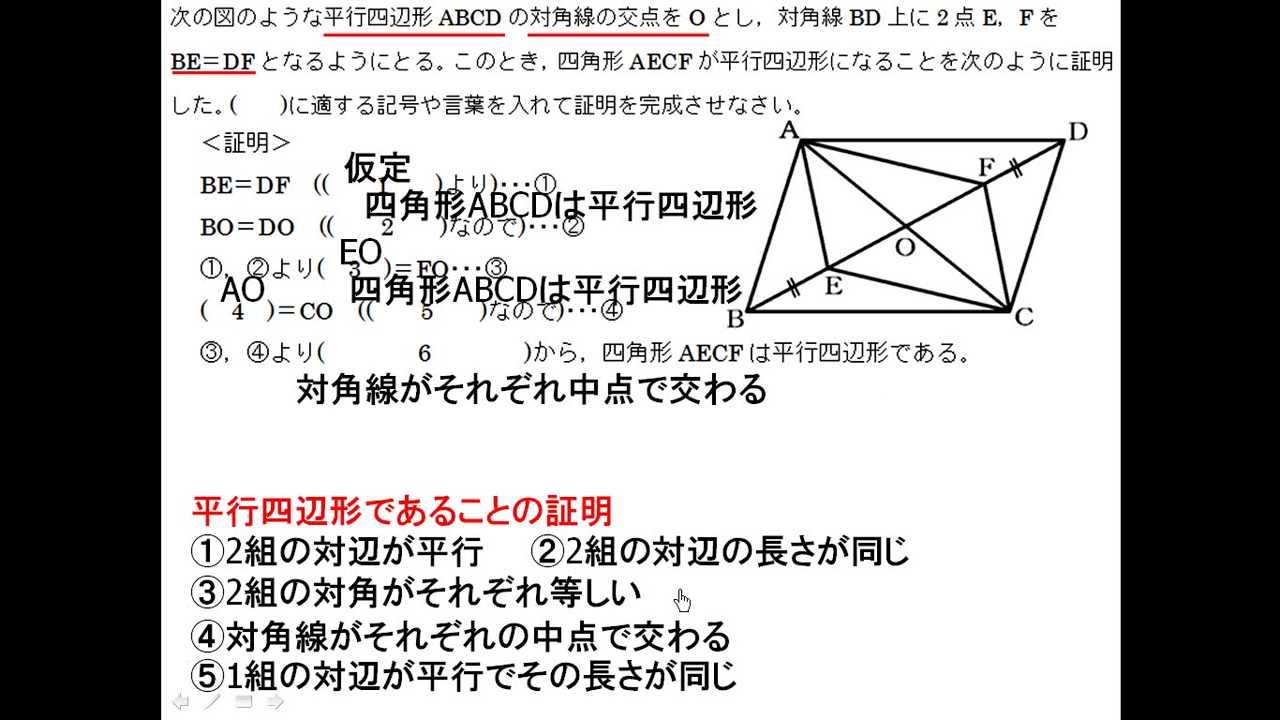
定義できる 特に, 平面のx 軸, y 軸の方向は右手系をなす 右手を左手に入れ換えて左手 系が定義される a b c 2 面積と体積 21 平行四辺形の面積 n 次元ベクトルa,b の作る平行四辺形(右下図) の面積をS とすれば, a,b のなす角をθ (0 ď θ ď π) として,平行四辺形の定義 ①定義 2組の対辺がそれぞれ平行である。 ②定理 2組の対辺がそれぞれ等しい。⑤ $\textcolor{blue}{1}$ 組の対辺が平行でその長さが等しい →定義・性質では出てこないけど、「平行四辺形であること」の証明ではよく使われます。 ①は平行四辺形の 定義 ②、③、④は平行四辺形の
Point〕いろいろな四角形 台形の定義 1組の対辺が平行である四角形 平行四辺形の定義 2組の対辺がそれぞれ平行な四角形 長方形の定義 4つの角がすべて等しい四角形(4つの角がみな直角である) ひし形の定義 4つの辺がすべて等しい四角形平行四辺形の定義は、「\(\boldsymbol{2}\) 組の向かい合う辺が平行な四角形を平行四辺形という 」になります。 また、平行四辺形になるためには、定義を含めて \(\boldsymbol{5}\) つの条件があります。簡単に説明すると、 「定義」 :こういうものを平行四辺形と呼ぼう! 「性質」 :平行四辺形と呼ばれるものには 共通してこんなことが言えるね! 「定理」 :性質の中で特に大切なこと! だから証明はいらないよ! こんな感じです。 例えば



数学 中2 73 平行四辺形の性質 Youtube




平行四辺形を中学生でもわかるように解説 性質 証明を即理解 高校生向け受験応援メディア 受験のミカタ
平行四辺形の定義から性質と条件をわかりやすく証明! 特に対角線の性質を押さえよう 21 6/15 図形のこと こんにちは、ウチダショウマです。 今日は、中学 2 2 年生の内容である 「平行四辺形になるための 5 5 つ の条件」 について、平行四辺形の定義から性質を証明し、そのあとで性質と条件が具体的にどう違うのかを詳しく見ていきましょう。もくじ 1 平行線で成り立つ中点連結定理とは何か 11 証明で中点連結定理が成り立つ理由を説明;2 中点でなくても、相似比から辺の長さを計算できる 21 平行線では、線の長さの比は同じ;



平行四辺形になる条件




数学 中2 74 平行四辺形になる条件 Youtube
平行四辺形の性質1 a b c d 平行四辺形の定義(ab//cd, ad//cb)から、2組の対辺はそれぞれ等しい(ab=cd, ad=cb)を証明する。 平行四辺形とは、 \(\bf{2}\) 組の向かい合う辺がそれぞれ平行な四角形 のことです。 まずはこの定義をしっかり覚えておきましょう。 平行四辺形の性質(定理)平行四辺形になる条件 四角形は、次の性質のどれかをもつと、平行四辺形である。 1 2組の向かいあう辺が、それぞれ平行である。(定義) 2 2組の向かいあう辺が、それぞれ等しい。(証明) 3 2組の向かいあう角が、それぞれ等しい。(証明)



Math 平行四辺形 平行四辺形になることの証明 働きアリ The 2nd




ねらい 平行四辺形の定義と性質を理解し 定義から導かれた性質を 三角形の合同条件などを使って証明することができる Ppt Download
関連記事 (21都立西)平行四辺形の難問証明 丁度良い角の二等分線公式(14年度沖縄県) 円周角と半径(中3円周角 証明プリント) 45(02年度茨城県改題) 範囲が大分削除された(オリジナル) そのため、対角線の長さ以外の情報がわかっていれば、もちろん平行四辺形の面積の求め方(\(\text{底辺} \times \text{高さ}\))でもひし形の面積を求められますよ。 平行四辺形とは?定義・条件・性質や面積の公式、証明問題平行四辺形の定義 2組の対辺がそれぞれ 平行な四角形 性質1 2組の対辺は それぞれ等しい 性質2 2組の対角は それぞれ等しい 性質3 対角線はそれぞれの 中点で交わる。




平行四辺形を中学生でもわかるように解説 性質 証明を即理解 高校生向け受験応援メディア 受験のミカタ




平行四辺形の定義から性質と条件をわかりやすく証明 特に対角線の性質を押さえよう 遊ぶ数学
向きは、平行四辺形の面に垂直で から a bc aの証明 b c& & && && u u a b a 2b 3 a 3b 2 e 1 a 3b 1 a 1b 3 e 2 a 1b 2 a 2b 1 e 3 & & & & & u 11 2 2 3 3 c ce ce ce & & & & aubc a 2b 3 a 3b 2 c 1 a 3b 1 a 1b 3 c 2 a 1b 2 a 2b 1 c 3 & &&(証明) 3 平行四辺形の対角線は、それぞれの中点で交わる 平行四辺形 (へいこうしへんけい、英 parallelogram)とは、2組の対辺がそれぞれ 平行 である 四角形 のことである 平行四辺形の定義は、2組の対辺がそれぞれ平行である 平行四辺形の性ユークリッド原論をどう読むか(3) 頁末 前 次 目次 ユークリッド原論 第1巻 命題1ー34(平行四辺形の対辺・対角・対角線) 平行四辺形・対角線 (平行四辺形と長斜方形とは同義) (平行四辺形の対角線は互いに他を2等分)




平行四辺形の定義 定理 性質 と証明問題 中学数学の図形 リョースケ大学
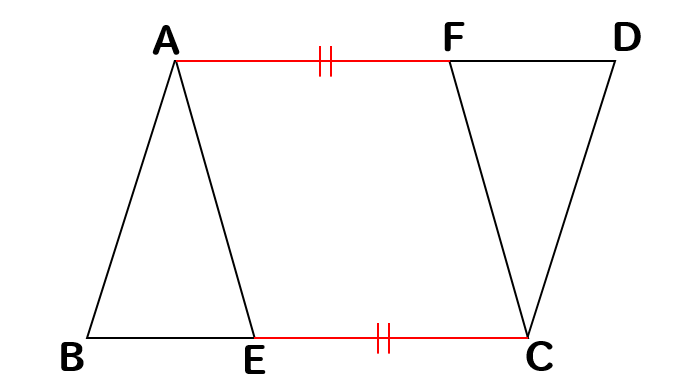



中学数学 平行四辺形の証明問題を徹底解説 数スタ
平行四辺形の定義となる。 (以下、定義1ー22の補足2(平行四辺形) という。) 命題1ー34は平行四辺形が長斜方形であることを論証している。 矩形のことを方形ともいう。 (以下、定義1ー22の補足3(方形) という。) <平行線> 定義1ー23(平行(線上のまとめに示したように「平行四辺形」の定義は「2組の向かい合う辺がそれぞれ平行である四角形」すなわち「 ad//bc , ab//dc 」が成り立つ四角形なので,仮定や結論が「平行四辺形」になっているときは「 ad//bc , ab//dc 」に置き換えるとよい この頁では平行線の性質について,証明の進め方 平行四辺形とひし形の違いってなに??←今回の記事 平行四辺形の角度、辺の長さを求める問題を解説! 平行四辺形の中から面積の等しい三角形を見つける問題を徹底解説! 等積変形三角形の面積問題と作図のやり方は?証明問題も紹介!



1




平行四辺形の定義と性質 証明問題の解き方 数学fun
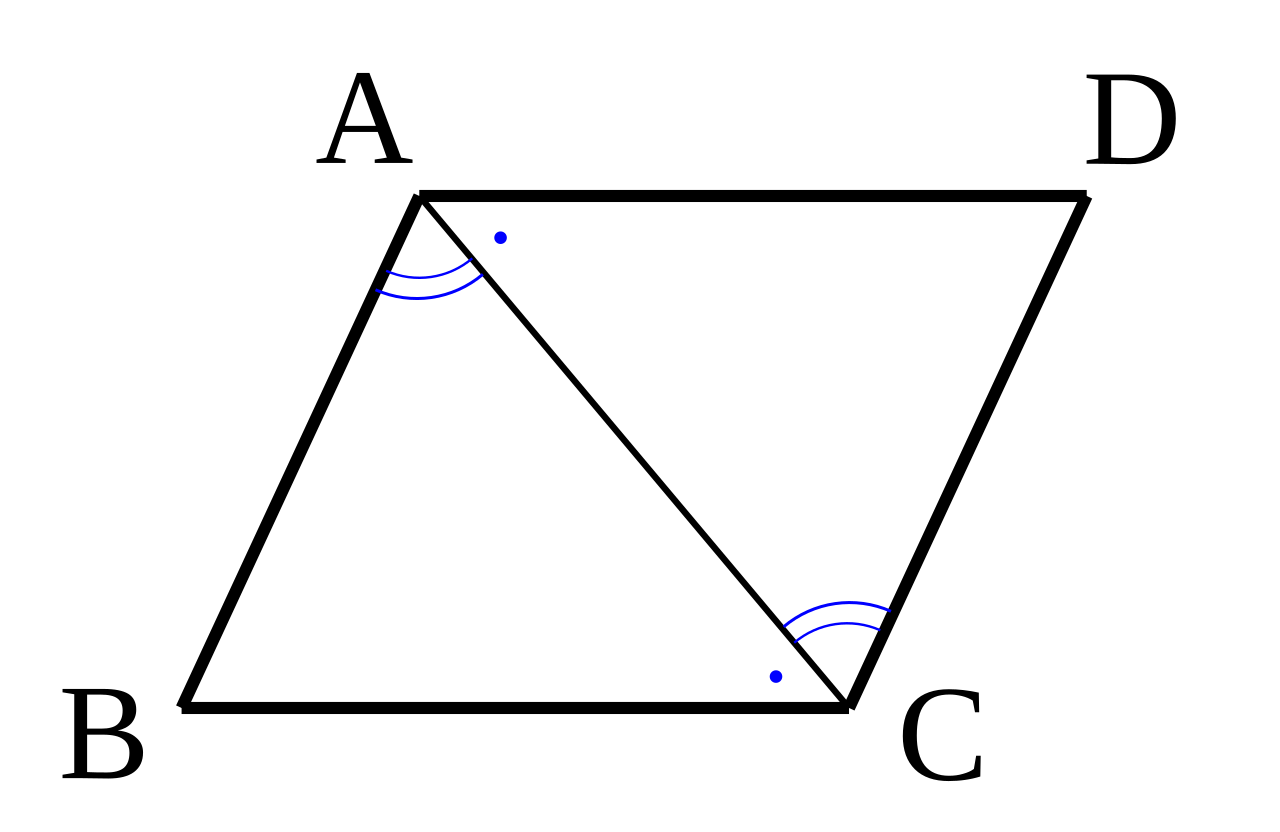
平行四辺形(1) 平行四辺形と直角三角形のパターンです。 直角三角形の合同と錯角を利用します。 平行四辺形(2) 平行四辺形を対角線を利用して証明するパターン。 平行四辺形であることを証明するのに例としてよく出る形ではあるのでしっかりと練習して平行四辺形になる条件の証明 2 2組の向かいあう辺が、それぞれ等しい。 ABCと CDAで、 AB=CD 1 BC=DA 2 AC=CA(共通) 3 1,2,3より3辺がそれぞれ等しいので、 ABC≡ CDA よって




平行四辺形の証明と角度を求める問題の解き方 現役塾講師のわかりやすい中学数学の解き方
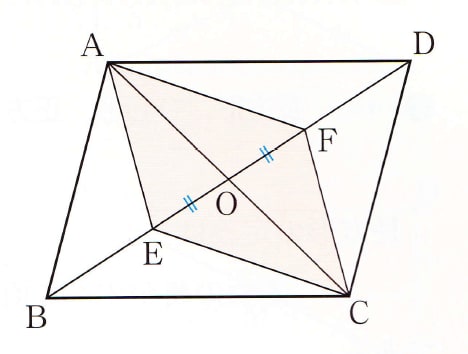



証明 は と が Takapの数学日記



平行 四辺 形 証明 平行四辺形になる条件の証明




3分で分かる 平行四辺形とは 定義や性質 成立条件をわかりやすく 合格サプリ




台形と平行四辺形を平行な辺の組の数で分類することは 原理的に不可能である 小学校4年生の算数 身勝手な主張




中学校数学 証明のコツ 年01月
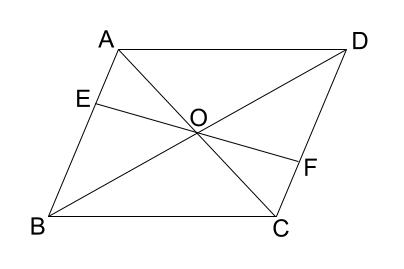



中学数学 証明 平行四辺形の性質の利用 中学数学の無料オンライン学習サイトchu Su



中点連結定理を使った平行四辺形であることの証明 教遊者



平行四辺形になるための証明1




中2数学 平行四辺形の性質の利用 練習編 映像授業のtry It トライイット




平行四辺形の定義から性質と条件をわかりやすく証明 特に対角線の性質を押さえよう 遊ぶ数学




平行四辺形を中学生でもわかるように解説 性質 証明を即理解 高校生向け受験応援メディア 受験のミカタ




平行四辺形 中学数学で遊ぶ 身勝手な主張



平行四辺形の証明がまったく分からない 新中3になる者です タイトル Yahoo 知恵袋
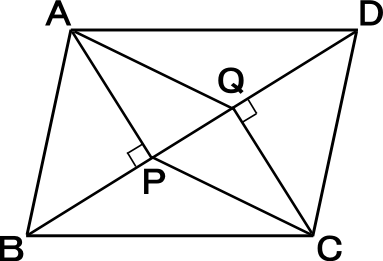



中学2年数学練習問題 平行四辺形になる条件と証明方法 図形と合同




平行四辺形を中学生でもわかるように解説 性質 証明を即理解 高校生向け受験応援メディア 受験のミカタ



3
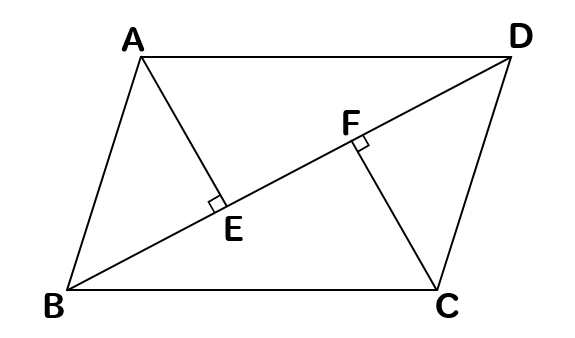



中学数学 平行四辺形の証明問題を徹底解説 数スタ



Math 平行四辺形 平行四辺形になることの証明 働きアリ The 2nd
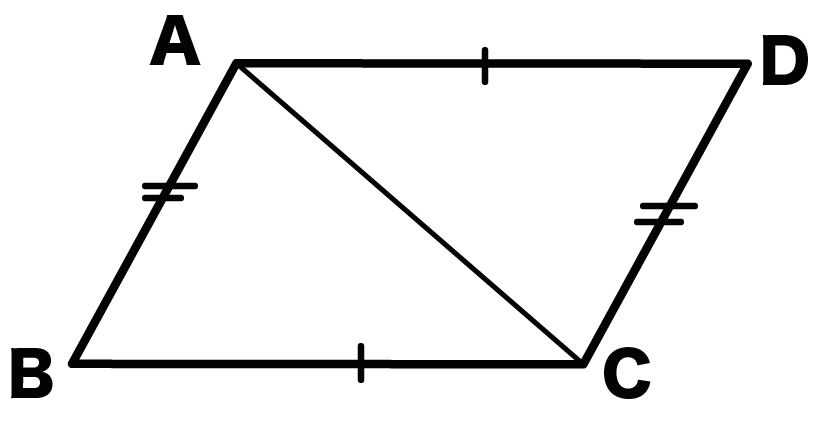



中2数学 平行四辺形の性質がわかる3つの証明 Qikeru 学びを楽しくわかりやすく




平行四辺形の性質 と ひし形の性質 を比べる とちぎeライブラリ



高校入試 英語 数学 学習 三角形と四角形 平行四辺形




平行四辺形の定理や定義 平行四辺形の覚えておきたい性質は4つ 中学や高校の数学の計算問題




中2数学 平行四辺形の証明で知っておくべき5つの方法 映像授業のtry It トライイット




中2数学 平行四辺形の証明で知っておくべき5つの方法 映像授業のtry It トライイット
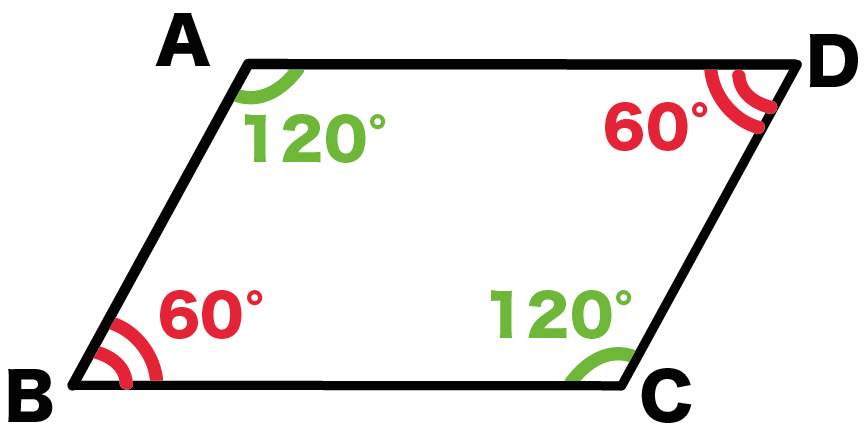



中2数学 平行四辺形の3つの性質 Qikeru 学びを楽しくわかりやすく




平行四辺形になる条件 小学生 中学生の勉強
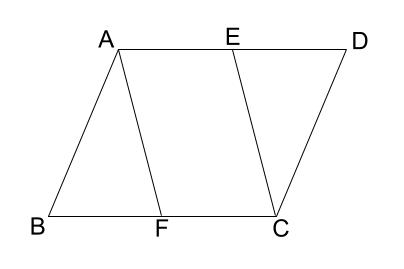



中学数学 証明 平行四辺形の性質の利用 中学数学の無料オンライン学習サイトchu Su
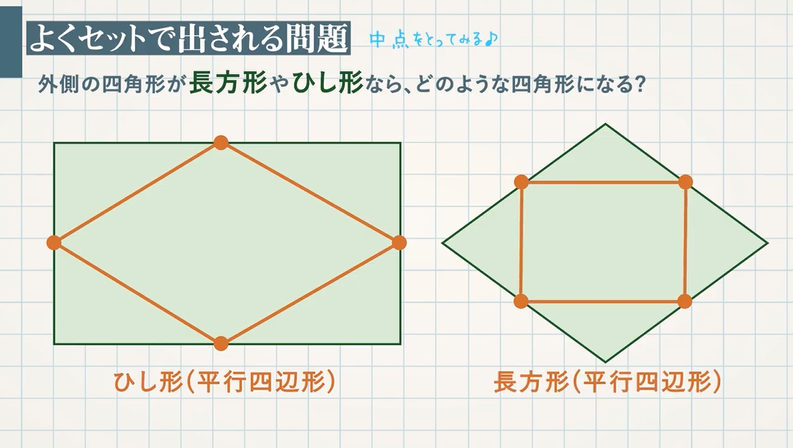



中点連結定理を使った平行四辺形であることの証明 教遊者




平行四辺形 中学数学で遊ぶ 身勝手な主張
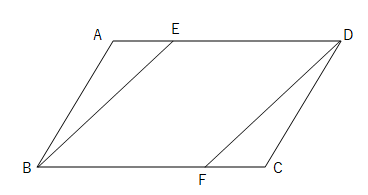



中2数学 平行四辺形の証明のポイントと練習問題 Examee
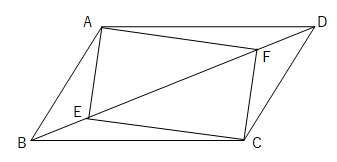



中2数学 平行四辺形の証明のポイントと練習問題 Examee
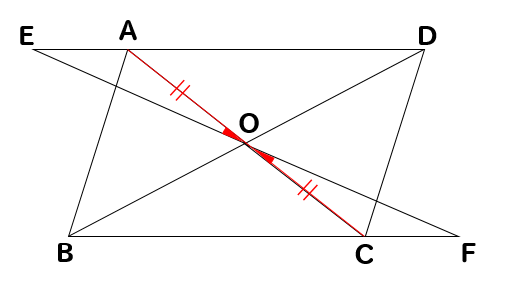



中学数学 平行四辺形の証明問題を徹底解説 数スタ



平行四辺形になる条件




平行四辺形の角度 辺の長さ 求め方を問題解説 数スタ
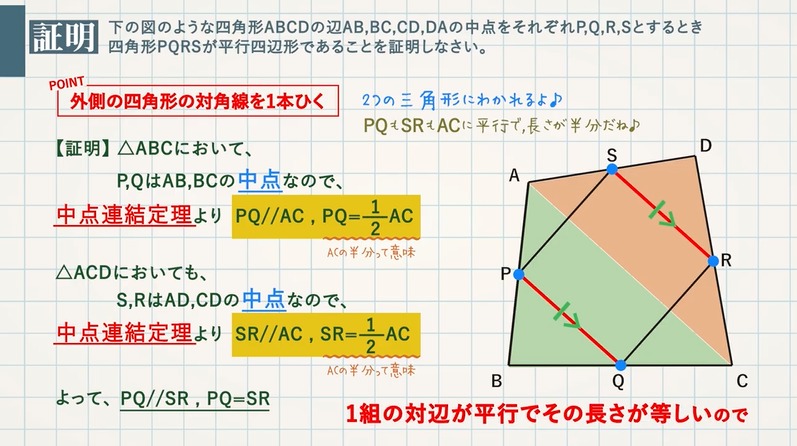



中点連結定理を使った平行四辺形であることの証明 教遊者




中2数学 平行四辺形の3大重要ポイント 映像授業のtry It トライイット




中学数学 平行四辺形の証明問題を徹底解説 数スタ
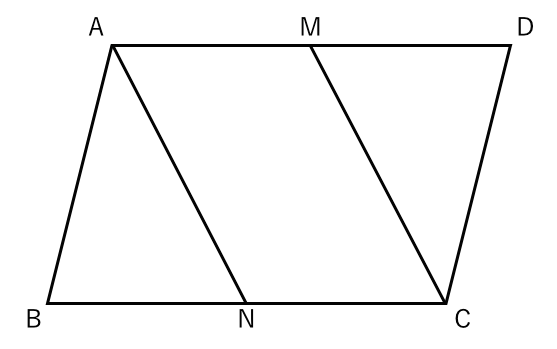



平行四辺形であることを証明する 苦手な数学を簡単に




三角形と四角形 平行四辺形であることの証明の仕方 中学数学 定期テスト対策サイト
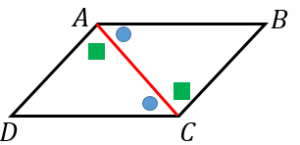



平行四辺形の3つの性質とその証明 具体例で学ぶ数学




中学数学 特別な平行四辺形について Clear



平行四辺形になる条件




高校数学b ベクトルの成分表示と平行四辺形 受験の月




平行四辺形の定義から性質と条件をわかりやすく証明 特に対角線の性質を押さえよう 遊ぶ数学
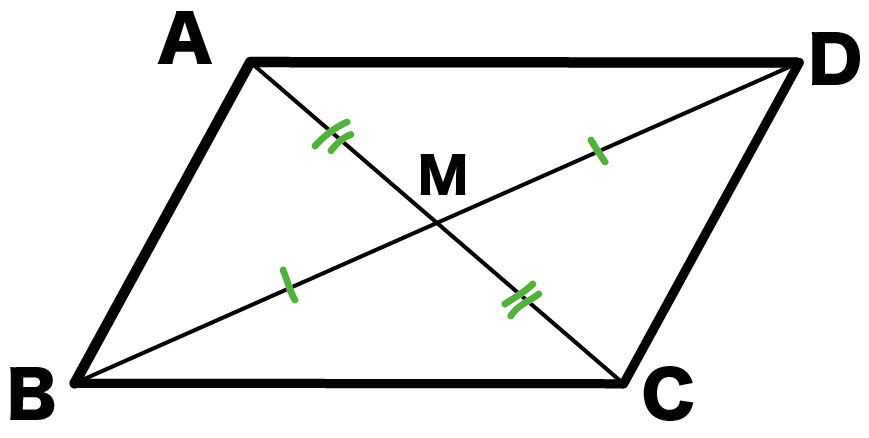



中2数学 平行四辺形の性質がわかる3つの証明 Qikeru 学びを楽しくわかりやすく
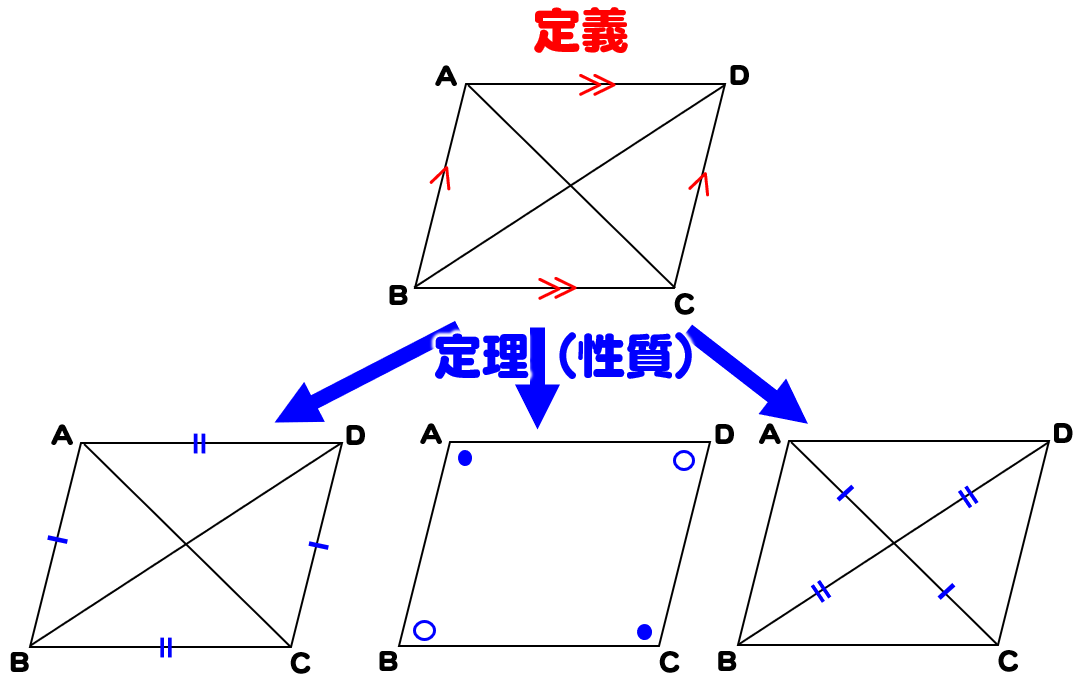



平行四辺形の定義と性質 証明問題の解き方 数学fun
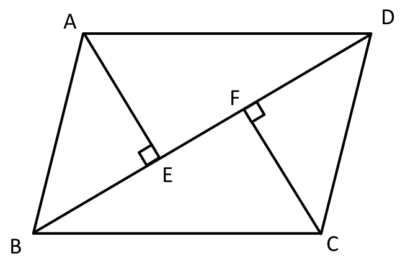



フロー 2 5 5 2 平行四辺形の性質を利用した証明




中2数学 平行四辺形の証明 練習編 映像授業のtry It トライイット
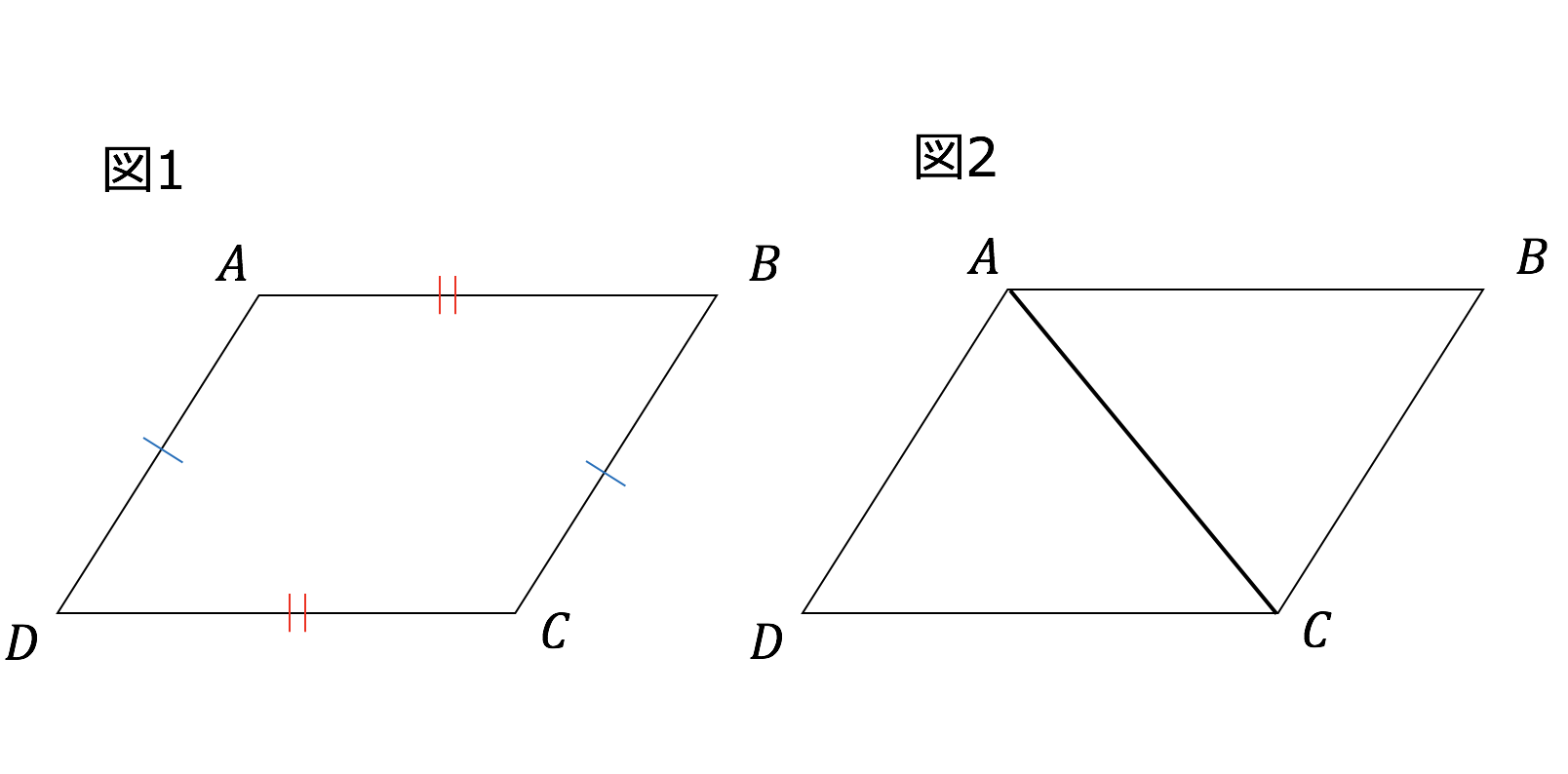



3分で分かる 平行四辺形とは 定義や性質 成立条件をわかりやすく 合格サプリ




平行四辺形になるための条件 Youtube
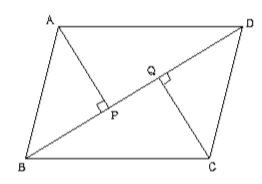



中2数学 平行四辺形の証明のポイントと練習問題 Examee




中2数学 平行四辺形の証明のポイントと練習問題 Examee
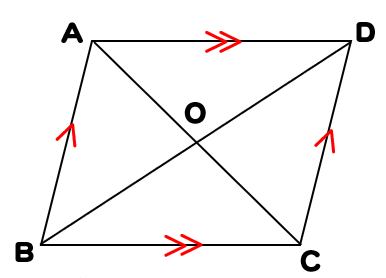



平行四辺形の定義と性質 証明問題の解き方 数学fun




中2 中2数学 平行四辺形の証明 授業ノート 中学生 数学のノート Clear




平行四辺形の定義 定理 性質 と証明問題 中学数学の図形 リョースケ大学



平行四辺形とは 定義 条件 性質や面積の公式 証明問題 受験辞典



平行 四辺 形 証明 平行四辺形になる条件の証明




平行四辺形の定義と性質 証明問題の解き方 数学fun




平行四辺形と証明 Youtube
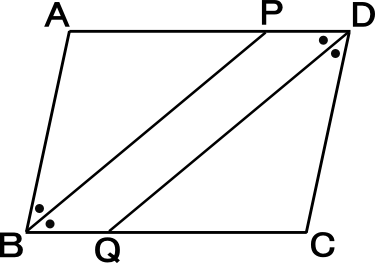



中学2年数学練習問題 平行四辺形になる条件と証明方法 図形と合同



平行四辺形になるための条件 まなびの学園
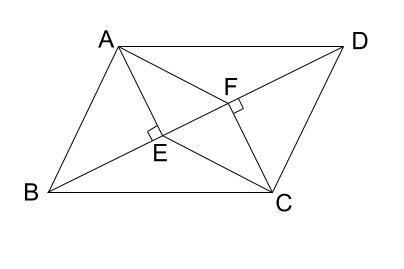



中学数学 平行四辺形になることの証明 その2 中学数学の無料オンライン学習サイトchu Su




平行四辺形を使った証明 Youtube



1




Math 平行四辺形 平行四辺形になることの証明 働きアリ




中2数学 平行四辺形の証明で知っておくべき5つの方法 映像授業のtry It トライイット




平行四辺形の定義 定理 性質 と証明問題 中学数学の図形 リョースケ大学



平行四辺形とは 定義 条件 性質や面積の公式 証明問題 受験辞典
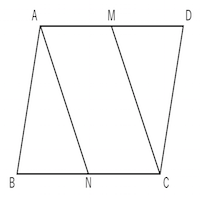



平行四辺形であることを証明する 苦手な数学を簡単に




中2数学 平行四辺形の3大重要ポイント 映像授業のtry It トライイット




平行四辺形の性質 長さ 角度の問題 無料で使える中学学習プリント




平行四辺形になることの証明 Youtube
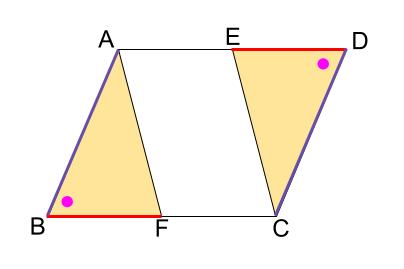



中学数学 証明 平行四辺形の性質の利用 中学数学の無料オンライン学習サイトchu Su



1



平行四辺形とは 定義 条件 性質や面積の公式 証明問題 受験辞典
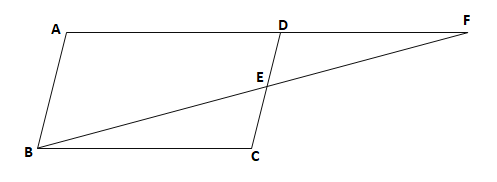



中2数学 平行四辺形の性質と証明の要点まとめノート 中学生勉強サイトあかね先生
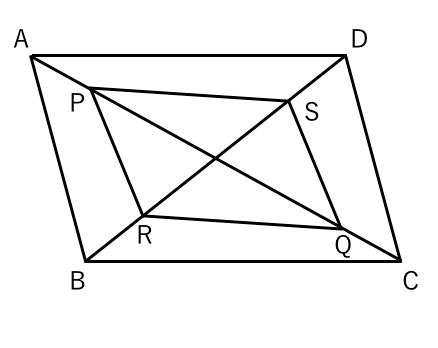



平行四辺形であることを証明する 苦手な数学を簡単に




中点連結定理とは 逆の証明や平行四辺形の問題もわかりやすく解説 遊ぶ数学
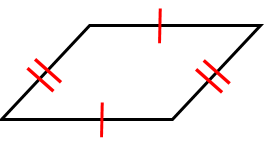



平行四辺形の3つの性質とその証明 具体例で学ぶ数学




簡単公式 平行四辺形の角度の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
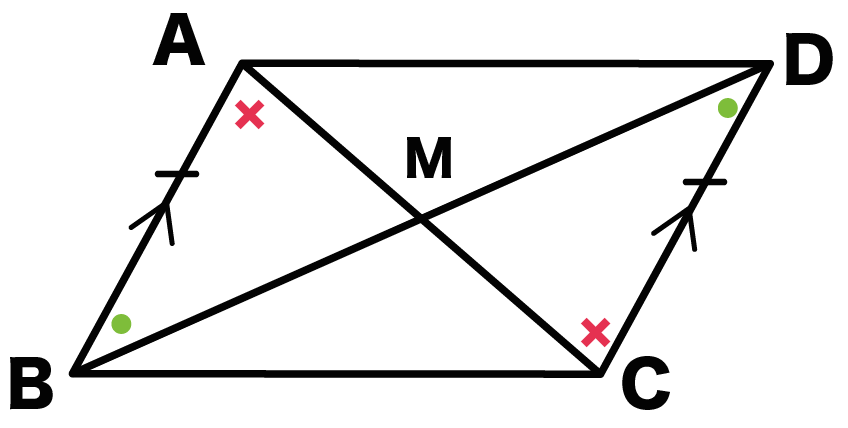



中2数学 平行四辺形の性質がわかる3つの証明 Qikeru 学びを楽しくわかりやすく




これ 問題の中に1つも平行ってワードがないのに どうして中点連結定理になるのか そし Clear




定義と定理 12月 年 光が丘中学校 ブログ 光が丘中学校




平行四辺形を中学生でもわかるように解説 性質 証明を即理解 高校生向け受験応援メディア 受験のミカタ



Math 平行四辺形 平行四辺形になることの証明 働きアリ The 2nd
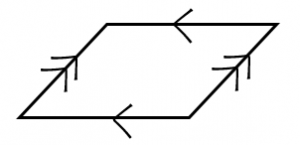



平行四辺形の3つの性質とその証明 具体例で学ぶ数学
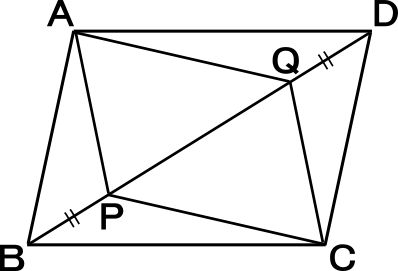



中学2年数学練習問題 平行四辺形になる条件と証明方法 図形と合同



平面図形の基礎



中2 数学 5 3 平行四辺形の証明 Youtube



平行 四辺 形 証明 平行四辺形になる条件の証明



平行四辺形とは 定義 条件 性質や面積の公式 証明問題 受験辞典



0 件のコメント:
コメントを投稿